Why is it that the number of petals in a flower is often associated with one of the following numbers: 3, 5, 8, 13, 21, or 34? Read on to explore the answer.

Have you heard about the famous Italian mathematician Leonardo Fibonacci and his Fibonacci number series given by the infinite elements: 0,1,1, 2,3,5,8,13,21,34,55,…;?

Nature in particular plants have no foreknowledge of this number sequence but surprisingly majority if not all petal arrangement of flowers carry these numbers! Below are some flowers that follow the Fibonacci number series.

In mathematics and the arts, two quantities are in the golden ratio (

) if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The figure on the right illustrates the geometric relationship. Expressed algebraically:

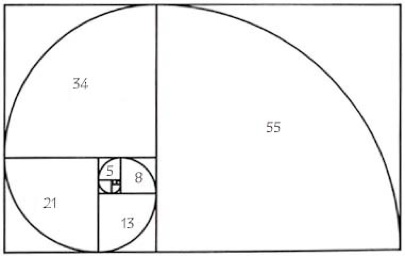
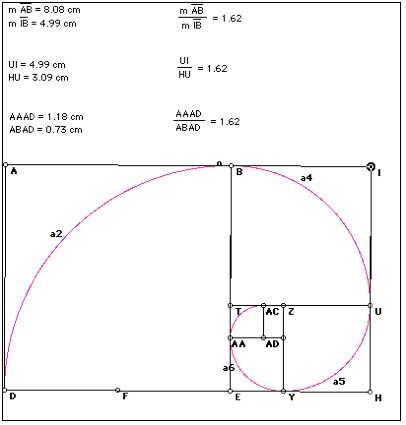
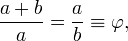
where the Greek letter phi represents the golden ratio. Its value is:

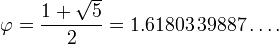
At least since the 20th century, many artists and architects have proportioned their works to approximate the golden ratio—especially in the form of the golden rectangle, in which the ratio of the longer side to the shorter is the golden ratio—believing this proportion to be aesthetically pleasing (see Applications and observations below). Mathematicians since Euclid have studied the properties of the golden ratio, including its appearance in the dimensions of a regular pentagon and in a golden rectangle, which can be cut into a square and a smaller rectangle with the same aspect ratio. The golden ratio has also been used to analyze the proportions of natural objects as well as man-made systems such as financial markets, in some cases based on dubious fits to data..